派克變換

　　派克變換（也譯作帕克變換，英語：Park's Transformation），是目前分析同步電動機運行最常用的一種坐標變換，由美國工程師派克（R.H.Park）在1929年提出。派克變換將定子的a,b,c三相電流投影到隨著轉子旋轉的直軸（d軸），交軸（q軸）與垂直于dq平面的零軸（0軸）上去，從而實現了對定子電感矩陣的對角化，對同步電動機的運行分析起到了簡化作用。

定義

　　派克正變換：

　　{\displaystyle{\mathbf{i}}_{dq0}={\mathbf{P}}{\mathbf{i}}_{abc}={\frac{2}{3}}\left[{\begin{array}{*{20}c}{\cos\theta}&{\cos\left({\theta-120^{\circ}}\right)}&{\cos\left({\theta+120^{\circ}}\right)}\\{-\sin\theta}&{-\sin\left({\theta-120^{\circ}}\right)}&{-\sin\left({\theta+120^{\circ}}\right)}\\{\frac{1}{2}}&{\frac{1}{2}}&{\frac{1}{2}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{i_{a}}\\{i_{b}}\\{i_{c}}\\\end{array}}\right]}{\displaystyle{\mathbf{i}}_{dq0}={\mathbf{P}}{\mathbf{i}}_{abc}={\frac{2}{3}}\left[{\begin{array}{*{20}c}{\cos\theta}&{\cos\left({\theta-120^{\circ}}\right)}&{\cos\left({\theta+120^{\circ}}\right)}\\{-\sin\theta}&{-\sin\left({\theta-120^{\circ}}\right)}&{-\sin\left({\theta+120^{\circ}}\right)}\\{\frac{1}{2}}&{\frac{1}{2}}&{\frac{1}{2}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{i_{a}}\\{i_{b}}\\{i_{c}}\\\end{array}}\right]}

　　逆變換：

　　{\displaystyle{\mathbf{i}}_{abc}={\mathbf{P}}^{-1}{\mathbf{i}}_{dq0}=\left[{\begin{array}{*{20}c}{\cos\theta}&{-\sin\theta}&1\\{\cos\left({\theta-120^{\circ}}\right)}&{-\sin\left({\theta-120^{\circ}}\right)}&1\\{\cos\left({\theta+120^{\circ}}\right)}&{-\sin\left({\theta+120^{\circ}}\right)}&1\\\end{array}}\right]\left[{\begin{array}{*{20}c}{i_gtlv65vdw}\\{i_{q}}\\{i_{0}}\\\end{array}}\right]}{\displaystyle{\mathbf{i}}_{abc}={\mathbf{P}}^{-1}{\mathbf{i}}_{dq0}=\left[{\begin{array}{*{20}c}{\cos\theta}&{-\sin\theta}&1\\{\cos\left({\theta-120^{\circ}}\right)}&{-\sin\left({\theta-120^{\circ}}\right)}&1\\{\cos\left({\theta+120^{\circ}}\right)}&{-\sin\left({\theta+120^{\circ}}\right)}&1\\\end{array}}\right]\left[{\begin{array}{*{20}c}{i_gtlv65vdw}\\{i_{q}}\\{i_{0}}\\\end{array}}\right]}

　　派克變換也作用在定子電壓與定子繞組磁鏈上：{\displaystyle{\mathbf{u}}_{dq0}={\mathbf{P}}{\mathbf{u}}_{abc}}{\displaystyle{\mathbf{u}}_{dq0}={\mathbf{P}}{\mathbf{u}}_{abc}}，{\displaystyle{\mathbf{\Psi}}_{dq0}={\mathbf{P}}{\mathbf{\Psi}}_{abc}}{\displaystyle{\mathbf{\Psi}}_{dq0}={\mathbf{P}}{\mathbf{\Psi}}_{abc}}

幾何解釋

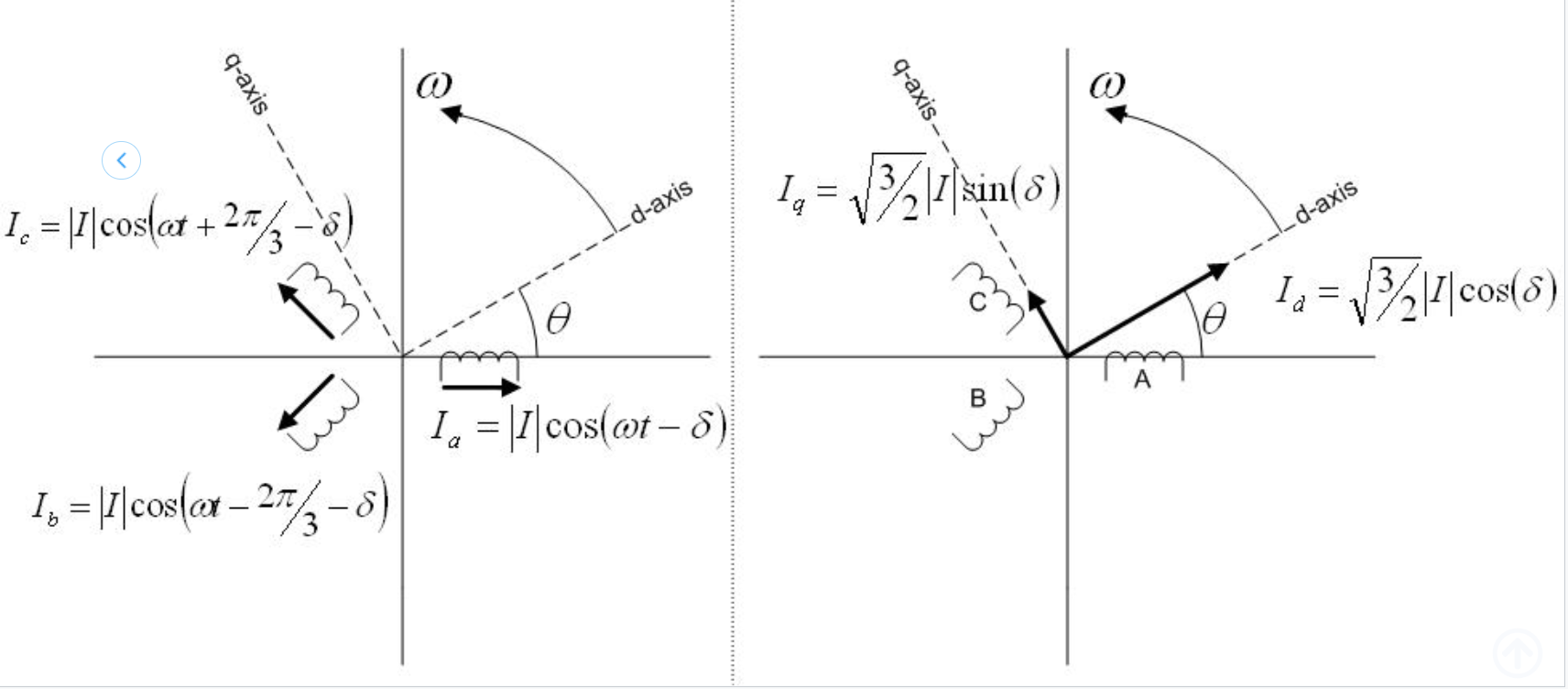
　　上圖描繪了派克變換的幾何意義，定子三相電流互成120度角，{\displaystyle\delta}\delta為定子電流落后于它們對應的相電壓的角度。直軸與交軸電流分別等于定子三相電流在d軸與q軸上的投影。（圖中的比例系數{\displaystyle{\sqrt{\frac{3}{2}}}}{\displaystyle{\sqrt{\frac{3}{2}}}}是由于圖中所采用的是正交形式的派克變換）d-q坐標系在空間中以角速度{\displaystyle\omega}\omega逆時針旋轉，故{\displaystyle\theta=\omega t}{\displaystyle\theta=\omega t}以d軸領先a相軸線的方向為正。當定子電流為三相對稱的正弦交流電時，{\displaystyle i_gtlv65vdw}{\displaystyle i_gtlv65vdw},{\displaystyle i_{q}}{\displaystyle i_{q}}為直流電流，{\displaystyle i_{0}=0}{\displaystyle i_{0}=0}。

用派克變換化簡同步發電機基本方程

變換后的磁鏈方程

　　磁鏈方程：

　　{\displaystyle\left[{\begin{array}{*{20}c}{{\mathbf{\Psi}}_{abc}}\\{{\mathbf{\Psi}}_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{{\mathbf{L}}_{SS}}&{{\mathbf{L}}_{SR}}\\{{\mathbf{L}}_{RS}}&{{\mathbf{L}}_{RR}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf{i}}_{abc}}\\{{\mathbf{i}}_{fDQ}}\\\end{array}}\right]}{\displaystyle\left[{\begin{array}{*{20}c}{{\mathbf{\Psi}}_{abc}}\\{{\mathbf{\Psi}}_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{{\mathbf{L}}_{SS}}&{{\mathbf{L}}_{SR}}\\{{\mathbf{L}}_{RS}}&{{\mathbf{L}}_{RR}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf{i}}_{abc}}\\{{\mathbf{i}}_{fDQ}}\\\end{array}}\right]}

　　上式中的電感系數矩陣{\displaystyle{{\mathbf{L}}_{SS}},{{\mathbf{L}}_{SR}},{{\mathbf{L}}_{RS}},{{\mathbf{L}}_{RR}}}{\displaystyle{{\mathbf{L}}_{SS}},{{\mathbf{L}}_{SR}},{{\mathbf{L}}_{RS}},{{\mathbf{L}}_{RR}}}事實上都含有隨時間變化的角度參數[1]，使得方程求解困難。

　　現對等式兩邊同時左乘{\displaystyle\left[{\begin{array}{*{20}c}{\mathbf{P}}&{}\\{}&{\mathbf{U}}\\\end{array}}\right]}{\displaystyle\left[{\begin{array}{*{20}c}{\mathbf{P}}&{}\\{}&{\mathbf{U}}\\\end{array}}\right]}，其中{\displaystyle{\mathbf{U}}}{\displaystyle{\mathbf{U}}}為三階單位矩陣。方程化為：

　　{\displaystyle\left[{\begin{array}{*{20}c}{{\mathbf{\Psi}}_{dq0}}\\{{\mathbf{\Psi}}_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{\mathbf{P}}&{}\\{}&{\mathbf{U}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{{\mathbf{L}}_{SS}}&{{\mathbf{L}}_{SR}}\\{{\mathbf{L}}_{RS}}&{{\mathbf{L}}_{RR}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{{\mathbf{P}}^{-1}}&{}\\{}&{\mathbf{U}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf{i}}_{abc}}\\{{\mathbf{i}}_{fDQ}}\\\end{array}}\right]}{\displaystyle\left[{\begin{array}{*{20}c}{{\mathbf{\Psi}}_{dq0}}\\{{\mathbf{\Psi}}_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{\mathbf{P}}&{}\\{}&{\mathbf{U}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{{\mathbf{L}}_{SS}}&{{\mathbf{L}}_{SR}}\\{{\mathbf{L}}_{RS}}&{{\mathbf{L}}_{RR}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{{\mathbf{P}}^{-1}}&{}\\{}&{\mathbf{U}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf{i}}_{abc}}\\{{\mathbf{i}}_{fDQ}}\\\end{array}}\right]}

　　{\displaystyle\left[{\begin{array}{*{20}c}{{\mathbf{\Psi}}_{dq0}}\\{{\mathbf{\Psi}}_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{{\mathbf{PL}}_{SS}{\mathbf{P}}^{-1}}&{{\mathbf{PL}}_{SR}}\\{{\mathbf{L}}_{RS}{\mathbf{P}}^{-1}}&{{\mathbf{L}}_{RR}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf{i}}_{dq0}}\\{{\mathbf{i}}_{fDQ}}\\\end{array}}\right]}{\displaystyle\left[{\begin{array}{*{20}c}{{\mathbf{\Psi}}_{dq0}}\\{{\mathbf{\Psi}}_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{{\mathbf{PL}}_{SS}{\mathbf{P}}^{-1}}&{{\mathbf{PL}}_{SR}}\\{{\mathbf{L}}_{RS}{\mathbf{P}}^{-1}}&{{\mathbf{L}}_{RR}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf{i}}_{dq0}}\\{{\mathbf{i}}_{fDQ}}\\\end{array}}\right]}

　　其中{\displaystyle{\mathbf{PL}}_{SS}{\mathbf{P}}^{-1}=\left[{\begin{array}{*{20}c}{L_gtlv65vdw}&{}&{}\\{}&{L_{q}}&{}\\{}&{}&{L_{0}}\\\end{array}}\right]\triangleq{\mathbf{L}}_{dq0}}{\displaystyle{\mathbf{PL}}_{SS}{\mathbf{P}}^{-1}=\left[{\begin{array}{*{20}c}{L_gtlv65vdw}&{}&{}\\{}&{L_{q}}&{}\\{}&{}&{L_{0}}\\\end{array}}\right]\triangleq{\mathbf{L}}_{dq0}}。

　　①變換后的電感系數都變為常數，可以假想dd繞組，qq繞組是固定在轉子上的，相對轉子靜止。

　　②派克變換陣對定子自感矩陣{\displaystyle{\mathbf{L}}_{SS}}{\displaystyle{\mathbf{L}}_{SS}}起到了對角化的作用，并消去了其中的角度變量。{\displaystyle{L_gtlv65vdw},{L_{q}},{L_{0}}}{\displaystyle{L_gtlv65vdw},{L_{q}},{L_{0}}}為其特征根。

　　③變換后定子和轉子間的互感系數不對稱，這是由于派克變換的矩陣不是正交矩陣。

　　④{\displaystyle{L_gtlv65vdw}}{\displaystyle{L_gtlv65vdw}}為直軸同步電感系數，其值相當于當勵磁繞組開路，定子合成磁勢產生單純直軸磁場時，任意一相定子繞組的自感系數。

變換后的電壓方程

　　電壓方程：

　　{\displaystyle\left[{\begin{array}{*{20}c}{{\mathbf{U}}_{abc}}\\{{\mathbf{U}}_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{{\mathbf{r}}_{S}}&{}\\{}&{{\mathbf{r}}_{R}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf{i}}_{abc}}\\{{\mathbf{i}}_{fDQ}}\\\end{array}}\right]+\left[{\begin{array}{*{20}c}{{\mathbf{\dot{\Psi}}}_{abc}}\\{{\mathbf{\dot{\Psi}}}_{fDQ}}\\\end{array}}\right]}{\displaystyle\left[{\begin{array}{*{20}c}{{\mathbf{U}}_{abc}}\\{{\mathbf{U}}_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{{\mathbf{r}}_{S}}&{}\\{}&{{\mathbf{r}}_{R}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf{i}}_{abc}}\\{{\mathbf{i}}_{fDQ}}\\\end{array}}\right]+\left[{\begin{array}{*{20}c}{{\mathbf{\dot{\Psi}}}_{abc}}\\{{\mathbf{\dot{\Psi}}}_{fDQ}}\\\end{array}}\right]}

　　現對等式兩邊同時左乘{\displaystyle\left[{\begin{array}{*{20}c}{\mathbf{P}}&{}\\{}&{\mathbf{U}}\\\end{array}}\right]}{\displaystyle\left[{\begin{array}{*{20}c}{\mathbf{P}}&{}\\{}&{\mathbf{U}}\\\end{array}}\right]}，其中{\displaystyle{\mathbf{U}}}{\displaystyle{\mathbf{U}}}為三階單位矩陣。方程化為：

　　{\displaystyle\left[{\begin{array}{*{20}c}{{\mathbf{U}}_{dq0}}\\{{\mathbf{U}}_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{{\mathbf{r}}_{S}}&{}\\{}&{{\mathbf{r}}_{R}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf{i}}_{dq0}}\\{{\mathbf{i}}_{fDQ}}\\\end{array}}\right]+\left[{\begin{array}{*{20}c}{{\mathbf{P{\dot{\Psi}}}}_{abc}}\\{{\mathbf{\dot{\Psi}}}_{fDQ}}\\\end{array}}\right]}{\displaystyle\left[{\begin{array}{*{20}c}{{\mathbf{U}}_{dq0}}\\{{\mathbf{U}}_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{{\mathbf{r}}_{S}}&{}\\{}&{{\mathbf{r}}_{R}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf{i}}_{dq0}}\\{{\mathbf{i}}_{fDQ}}\\\end{array}}\right]+\left[{\begin{array}{*{20}c}{{\mathbf{P{\dot{\Psi}}}}_{abc}}\\{{\mathbf{\dot{\Psi}}}_{fDQ}}\\\end{array}}\right]}

　　由{\displaystyle{\mathbf{\Psi}}_{dq0}={\mathbf{P\Psi}}_{abc}}{\displaystyle{\mathbf{\Psi}}_{dq0}={\mathbf{P\Psi}}_{abc}}，

　　對兩邊求導，得{\displaystyle{\mathbf{\dot{\Psi}}}_{dq0}={\mathbf{{\dot{P}}\Psi}}_{abc}+{\mathbf{P{\dot{\Psi}}}}_{abc}}{\displaystyle{\mathbf{\dot{\Psi}}}_{dq0}={\mathbf{{\dot{P}}\Psi}}_{abc}+{\mathbf{P{\dot{\Psi}}}}_{abc}}，

　　所以{\displaystyle{\mathbf{P{\dot{\Psi}}}}_{abc}={\mathbf{\dot{\Psi}}}_{dq0}-{\mathbf{{\dot{P}}\Psi}}_{abc}={\mathbf{\dot{\Psi}}}_{dq0}-{\mathbf{{\dot{P}}P}}^{-1}{\mathbf{\Psi}}_{dq0}}{\displaystyle{\mathbf{P{\dot{\Psi}}}}_{abc}={\mathbf{\dot{\Psi}}}_{dq0}-{\mathbf{{\dot{P}}\Psi}}_{abc}={\mathbf{\dot{\Psi}}}_{dq0}-{\mathbf{{\dot{P}}P}}^{-1}{\mathbf{\Psi}}_{dq0}}

　　其中{\displaystyle{\mathbf{{\dot{P}}P}}^{-1}=\left[{\begin{array}{*{20}c}{}&\omega&{}\\{-\omega}&{}&{}\\{}&{}&{}\\\end{array}}\right]}{\displaystyle{\mathbf{{\dot{P}}P}}^{-1}=\left[{\begin{array}{*{20}c}{}&\omega&{}\\{-\omega}&{}&{}\\{}&{}&{}\\\end{array}}\right]}，令{\displaystyle{\mathbf{S}}={\mathbf{{\dot{P}}P}}^{-1}{\mathbf{\Psi}}_{dq0}=\left[{\begin{array}{*{20}c}{}&\omega&{}\\{-\omega}&{}&{}\\{}&{}&{}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{\Phi _gtlv65vdw}\\{\Phi _{q}}\\{\Phi _{0}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{\omega\Psi _{q}}\\{-\omega\Psi _gtlv65vdw}\\{}\\\end{array}}\right]}{\displaystyle{\mathbf{S}}={\mathbf{{\dot{P}}P}}^{-1}{\mathbf{\Psi}}_{dq0}=\left[{\begin{array}{*{20}c}{}&\omega&{}\\{-\omega}&{}&{}\\{}&{}&{}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{\Phi _gtlv65vdw}\\{\Phi _{q}}\\{\Phi _{0}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{\omega\Psi _{q}}\\{-\omega\Psi _gtlv65vdw}\\{}\\\end{array}}\right]}

　　于是有{\displaystyle\left[{\begin{array}{*{20}c}{{\mathbf{U}}_{dq0}}\\{{\mathbf{U}}_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{{\mathbf{r}}_{S}}&{}\\{}&{{\mathbf{r}}_{R}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf{i}}_{dq0}}\\{{\mathbf{i}}_{fDQ}}\\\end{array}}\right]+\left[{\begin{array}{*{20}c}{{\mathbf{\dot{\Psi}}}_{dq0}}\\{{\mathbf{\dot{\Psi}}}_{fDQ}}\\\end{array}}\right]-\left[{\begin{array}{*{20}c}{\mathbf{S}}\\{}\\\end{array}}\right]}{\displaystyle\left[{\begin{array}{*{20}c}{{\mathbf{U}}_{dq0}}\\{{\mathbf{U}}_{fDQ}}\\\end{array}}\right]=\left[{\begin{array}{*{20}c}{{\mathbf{r}}_{S}}&{}\\{}&{{\mathbf{r}}_{R}}\\\end{array}}\right]\left[{\begin{array}{*{20}c}{-{\mathbf{i}}_{dq0}}\\{{\mathbf{i}}_{fDQ}}\\\end{array}}\right]+\left[{\begin{array}{*{20}c}{{\mathbf{\dot{\Psi}}}_{dq0}}\\{{\mathbf{\dot{\Psi}}}_{fDQ}}\\\end{array}}\right]-\left[{\begin{array}{*{20}c}{\mathbf{S}}\\{}\\\end{array}}\right]}

　　上式右邊第一項為繞組電阻的壓降，第二項為變壓器電勢，第三項為發電機電勢或旋轉電勢。

關于派克變換，小編為大家就分享這些。歡迎聯系我們合運電氣有限公司，以獲取更多相關知識。